Question

Which of the following is a step in simplifying the expression x multiplied by y to the power of 4 over x to the power of negative 5 multiplied by y to the power of 5, the whole to the power of negative 3.?

A:
x to the power of negative 3 multiplied by y, the whole over x to the power of negative 8 multiplied by y to the power of 2.
B:
x to the power of negative 3 multiplied by y to the power of negative 12, the whole over x to the power of negative 5 multiplied by y to the power of 5.
C:
x to the power of negative 3 multiplied by y, the whole over x to the power of negative 5 multiplied by y to the power of 5.
D:
x to the power of negative 3 multiplied by y to the power of negative 12, the whole over x to the power of 15 multiplied by y to the power of negative 15.

Answer 1

D: x to the power of negative 3 multiplied by y to the power of negative 12, the whole over x to the power of 15 multiplied by y to the power of negative 15.

Explanation:

Given:

`((xy^4)/(x^(-5)y^5))^(-3)`

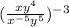
Now We need to Simplify the given expression;

So by using Law of Indices which states

`(a^m)^n=a^(mn)`

So By applying the same law in above expression we get;

`(x^(-3)y^(4*-3))/(x^(-5*-3)y^(5*-3))\\\\=(x^(-3)y^(-12))/(x^(15)y^(-15))`

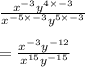
Hence the correct option from given option is:

x to the power of negative 3 multiplied by y to the power of negative 12, the whole over x to the power of 15 multiplied by y to the power of negative 15.