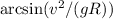Question

Suppose a car of mass m is moving at a constant speed v of

30m/s around a curve whose radius R is 170 m. What angle ofbank

makes reliance on friction unnecessary?

Answer 1

The angle of banked curve that makes the reliance on friction unnecessary is

`\arcsin(v^2/(gR))`

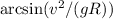
Step-by-step explanation:

In order the car to stay on the curve without friction, the net force in the direction of radius should be equal or smaller than the centripetal force. Otherwise the car could slide off the curve.

The only force in the direction of radius is the sine component of the weight of the car

`w_r = mg\sin(\theta)`

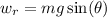
The cosine component is equivalent to the normal force, which we will not be using since friction is unnecessary.

Newton’s Second Law states that

`F_(net) = ma = mg\sin(\theta)\\\sin(\theta) = a/g`

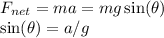
Also, the car is making a circular motion:

`a = (v^2)/(R)`

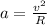
Combining the equations:

`\sin(\theta) = (a)/(g) = (v^2/R)/(g) = (v^2)/(gR)`

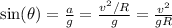
Finally the angle is

`\arcsin(v^2/(gR))`