Step-by-step explanation:
It is given that initially pressure of ideal gas is 4.00 atm and its temperature is 350 K. Let us assume that the final pressure is
 and final temperature is
and final temperature is
 .
.
(a) We know that for a monoatomic gas, value of
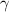 is \frac{5}{3}[/tex].
is \frac{5}{3}[/tex].
And, in case of adiabatic process,
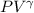 = constant
= constant
also, PV = nRT
So, here
 = 350 K,
= 350 K,
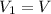 , and
, and
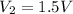
Hence,


 = 267 K
= 267 K
Also,
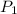 = 4.0 atm,
= 4.0 atm,
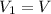 , and
, and
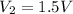
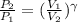
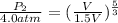
 = 2.04 atm
= 2.04 atm
Hence, for monoatomic gas final pressure is 2.04 atm and final temperature is 267 K.
(b) For diatomic gas, value of
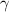 is \frac{7}{5}[/tex].
is \frac{7}{5}[/tex].
As,
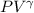 = constant
= constant
also, PV = nRT
 = 350 K,
= 350 K,
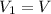 , and
, and
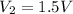

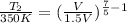
 = 289 K
= 289 K
And,
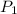 = 4.0 atm,
= 4.0 atm,
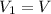 , and
, and
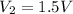
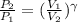
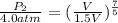
 = 2.27 atm
= 2.27 atm
Hence, for diatomic gas final pressure is 2.27 atm and final temperature is 289 K.