Question

A 15.0-mW laser puts out a narrow beam 2.00 mm indiameter.

What is the average (rms) value of the magneticfield?

Answer 1

Step-by-step explanation:

It is known that formula for energy per unit area per unit time is as follows.

S =
`(P)/(A)`

=
`(P)/(\pi * r^(2)) = (4P)/(\pi d^(2))`

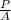
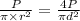
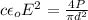
`c \epsilon_(o) E^(2) = (4P)/(\pi d^(2))`

E =
`\sqrt{(4P)/(\pi d^(2) c \epsilon_(o))}`

Now, putting the values we will calculate the electric field as follows.

E =
`\sqrt{(4P)/(\pi d^(2) c \epsilon_(o))}`

=
`\sqrt{(4 * 15 * 10^(-3) W)/(3.14 * (2mm * (1m)/(1000 mm))^(2) * 3 * 10^(8) * 8.85 * 10^(-12))}`

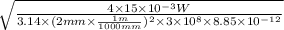
= 1341.03 V/m

Now, we will calculate the average magnetic field as follows.

B =
`(E)/(c)`

=
`(1341.03 V/m)/(3 * 10^(8) m/s)`

=
`4.47 * 10^(-6)` T

=
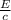
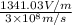
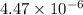`4.47 \mu T`

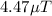
Thus, we can conclude that the average (rms) value of the magnetic field is
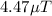`4.47 \mu T`.