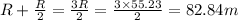Answer:
Step-by-step explanation:
Given
Launch velocity
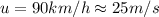
inclination
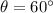
At highest point the projectile exploded such that one part falls vertically downward and other part travel in a trajectory such that it land on earth at distance of x m from original position of center of mass
As the force is internal so center of mass of the system will remain at the same position. So particle will land at such spots such that com will remain at Range of Projectile.
Original Position of center mass is given by the Range of Projectile
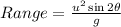

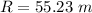
at Highest position distance of first part from center of mass will be
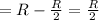
product of mass and distance from center of mass should be same therefore
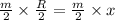
thus

i.e. Second part is at a distance of
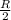 from center of mass
from center of mass
From gun it is