There are multiple different trees that are possible here. One way is to follow these steps
----------
Step 1) Select the smallest prime number 2 and see if it can be divided into 504. It turns out it can since 504/2 = 252 is a whole number. In other words, 2*252 = 504. Under the "504", write "2" and "252" so that the two new values are spaced out. Draw a line that connects the 504 to the 2. Also, draw a line that connects the 504 to the 252. These lines help us see that 504 factors into 2*252. Check out the diagram below to see what I mean.
----------
Step 2) See if 2 can go into 252. It can since 252/2 = 126. Write "2" and "126" under the "252". Make sure there is enough space. Draw lines to connect 252 to 2 and to 126 as well.
----------
Step 3) Like the previous steps, see if 2 goes into 126. It can since 126/2 = 63. So 2*63 = 126 which means we will have "2" and "63" under the 126. Connect these new values to the 63.
----------
Step 4) Sadly 2 doesn't go into 63 (becuse 63/2 = 31.5 is not a whole number). Move up to the next prime 3 and see if 3 goes into 63. It does since 63/3 = 21. So 3*21 = 63. Draw lines connecting these new values to 63.
----------
Step 5) Check to see if 2 goes into 21. It does not because 21/2 = 10.5; however 3 does because 21/3 = 7. We have 3*7 = 21. We've reached the end of the factor tree because both 3 and 7 are prime. Circle all of the prime numbers
----------
All the circled prime numbers can be multiplied together to get the original number 504 back again
504 = 2*2*2*3*3*7
which can be written more compactly like this
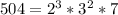
-----------
This is not the only factor tree possible. However, you will get the same primes, and the same number of each of them,, no matter what factor tree you generate for the number 504.