Answer:
The number of ways to select 12 jurors are 86493225.
The number of ways to select 2 alternates are 306.
Explanation:
Consider the provided information.
In many courts, 12 jurors are chosen from a pool of 30 perspective jurors.
Part (A): In how many ways can 12 jurors be chosen from the pool of 30 perspective jurors?
Since order doesn't matter so we will use combination.
Use the formula for combination
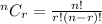
Substitute n=30 and r=12 in above formula.
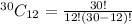
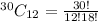
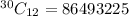
Hence, the number of ways to select 12 jurors are 86493225.
Part (B) Once the 12 jurors are selected, 2 alternates are selected. The order of the alternates is specified. If a selected juror cannot complete the trial, the first alternate is called on to fill that jury spot. In how many ways can the 2 alternates be chosen after the 12 jury members have been chosen?
Here 12 jury members have been chosen, so 30-12=18 perspective jurors are left.
From 18 perspective jurors we need to select 2 alternates.
Since the order of the alternates matter so we will use permutation:
The formula for permutation is:
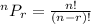
Substitute n=18 and r=2 in above formula.
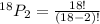
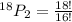
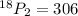
Hence, the number of ways to select 2 alternates are 306.