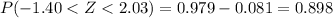Answer:
a)
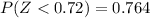
b)
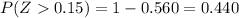
c)
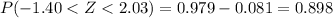
Explanation:
a)To the left of z = 0.72.
For this case the shaded area is on the figure 1 attached.
And we can find the area with the normal standard table of with the following excel code:
=NORM.DIST(0.72,0,1,TRUE)
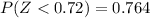
b)To the right of z = 0.15.
For this case the shaded area is on the figure 2 attached.
And we can find the area with the normal standard table of with the following excel code:
=1-NORM.DIST(0.15,0,1,TRUE)
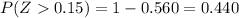
c)Between z = -1.40 and z = 2.03.
For this case the shaded area is on the figure 3 attached.
And we can find the area with the normal standard table of with the following excel code:
=NORM.DIST(2.03,0,1,TRUE)-NORM.DIST(-1.40,0,1,TRUE)