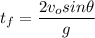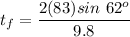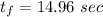Question

2. An archer shoots an arrow at 83.0 m/s at a 62.0 degree angle. If the ground is flat, how much time is the arrow in the air?

Answer 1

t=14.96 sec

Step-by-step explanation:

Diagonal Launch

It's a physical event that happens where an object is thrown in free air (no friction) forming an angle with the horizontal reference. The object then describes a path called a parabola.

The object will reach its maximum height and then return to the height from which it was launched. The equation for the height is :

`\displaystyle y=y_o+v_osin\theta \ t-(gt^2)/(2)`

Where vo is the initial speed,
`\theta` is the angle, t is the time and g is the acceleration of gravity .

In this problem we'll assume the arrow was launched from the ground level (won't consider the archer's height). Thus
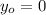`y_o=0`, and:

`\displaystyle y=v_osin\theta \ t-(gt^2)/(2)`

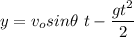
The value of y is zero twice: when t=0 (at launching time) and in t=
`t_f` when it goes back to the ground. We need to find that time
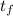`t_f` by making
`y=0`

`\displaystyle 0=v_osin\theta\ t_f-(gt_f^2)/(2)`

Dividing by
`t_f`

`\displaystyle v_osin\theta=(gt_f)/(2)`

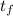
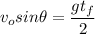
Then we find the total flight time as

`\displaystyle t_f=(2v_osin\theta)/(g)`

`\displaystyle t_f=(2(83)sin\ 62^o)/(9.8)`

`\displaystyle t_f=14.96\ sec`