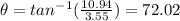Answer:
a) Figure attached
b)
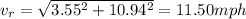
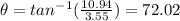
Explanation:
Part a
See the figure attached.
Part b
For this case first we need to find the vectors of velocity for the boat and the wind like this:
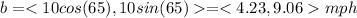
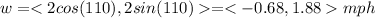
And now if we want to find the resulting velocity we just need to add the vector:
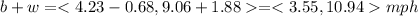
And the resultant magnitude would be:
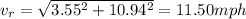
And if we want the resultant angle we can do this: