Answer:
98.64ft
Explanation:
Well, according to which is described in the question, the problem can be solved using simple trigonometry, applying the Law of Sines and acknowledging what an angle of depression is.
Firstly, an angle of depression is "The angle below horizontal that an observer must look to see an object that is lower than the observer" Angle of Depression (2020), in Mathwords.
A sketch obtained from the question is attached to the solution. See below.
It is telling us that we can depict a right angle. The horizontal line forms an angle of 90 degrees with h. Since we know that the angle of depression is 16 degrees, the angle formed by the line that connects the Sun, the tower and the end of the shadow with h is
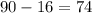 degrees, since the latter and the angle of depression are complementary angles (they sum 90 degrees).
degrees, since the latter and the angle of depression are complementary angles (they sum 90 degrees).
Likewise, knowing that the sum of the inner angles of a triangle is 180°, the value for the remaining angle is
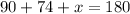 or
or
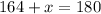 , so
, so
 .
.
Well, looking at the sketch, we can calculate the height of the transmitting tower (h) using the Law of Sines, that is:
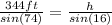
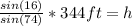
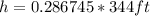
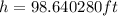
Then, the tower is, approximately, 98.64ft high.