Question

Compare the graphs of the function, ????(x) = −2(x + 3)^2 + 2 and ????(x) = 5(x + 3)^2 + 2. What do the graphs have

in common? How are they different?

Answer 1

Similarity: Both functions has same vertex at point
`(-3,2)`.

Difference:
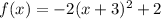`f(x)=-2(x+3)^2+2` is downward opening parabola, while
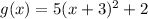`g(x)=5(x+3)^2+2` is an upward opening parabola.

Explanation:

We have been given two functions as:
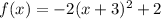`f(x)=-2(x+3)^2+2` and
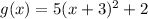`g(x)=5(x+3)^2+2`. We are asked to compare the graphs of the given function.

We know that standard form of a parabola with vertex at point (h,k) is in format
`y=a(x-h)^2+k`.

Let us find the similarity in both graphs.

• Upon comparing both functions with standard form of a parabola, we can see that vertex of the both parabolas is at point
  `(-3,2)`.

Let us find the difference in both graphs.

We can see that leading coefficient of
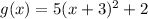`g(x)=5(x+3)^2+2` is positive, so it will be an upward opening parabola.

We can also see that leading coefficient of
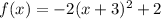`f(x)=-2(x+3)^2+2` is negative, so it will be a downward opening parabola.