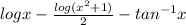Question

Integrate 1 - x / x(x2 + 1) d x by partial fractions.

Answer 1

`log x-(log(x^(2)+1) )/(2)-tan^(-1) x`

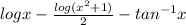
Explanation:

step 1:- by using partial fractions

`[tex](1-x)/(x(x^(2)+1) ) =(A(x^(2)+1)+(Bx+C)(x )/(x(x^(2)+1) )`......(1)

step 2:-

solving on both sides

`1-x=A(x^(2) +1)+(Bx+C)x......(2)`

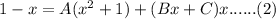
substitute x =0 value in equation (2)

1=A(1)+0

A=1

comparing x^2 co-efficient on both sides (in equation 2)

0 = A+B

0 = 1+B

B=-1

comparing x co-efficient on both sides (in equation 2)

-1 = C

step 3:-

substitute A,B,C values in equation (1)

now

`\\\int\limits^ {} \, (1-x)/(x(x^(2)+1) ) d x </p><p>=\int\limits^ {} (1)/(x) d x +\int\limits^ {} (-x)/(x^(2)+1 )  d x -\int\limits (1)/(x^(2)+1 )  d x`

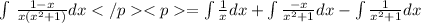
by using integration formulas

i) by using
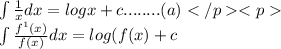`\int\limits (1)/(x)   d x =log x+c........(a)</p><p>\\\int\limits (f^(1)(x) )/(f(x)) d x= log(f(x)+c\\`.....(b)

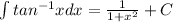`\int\limits tan^(-1)x  dx =(1)/(1+x^(2) ) +C`.....(c)

step 4:-

by using above integration formulas (a,b,and c)

we get answer is

`log x-(log(x^(2)+1) )/(2)-tan^(-1) x`