Question

In the triangle ABC, if side a is 3, side b is 4 and side c is 5, what is the cosine of the smallest angle?

Answer 1

Cosine of the smallest angle is 4/5.

Explanation:

It is given that in the triangle ABC, side a is 3, side b is 4 and side c is 5.

Sum of squares of two smaller sides.

`3^2+4^2=9+16=25`

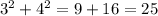
Sum of squares of largest sides.

`5^2=25`

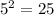
Since sum of squares of two smaller sides is equal to sum of squares of largest sides, therefore triangle ABC is a right angle triangle.

Hypotenuse = 5 units.

In a right angle triangle, the smallest angle has shortest opposite side.

Shortest side is a=3 It means angle A is smallest.

`\cos \theta = (adjacent)/(hypotenuse)`

`\cos (A) = (AC)/(AB)`

`\cos (A) = (4)/(5)`

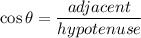
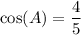
Therefore, the cosine of the smallest angle is 4/5.