Question

Find exact values of the six trigonometric functions for

theangle 300 degrees (rationalizing the denominator).

Answer 1

Since, the six main trigonometric functions are:

• Sine (sin)
• Cosine (cos)
• Tangent (tan)
• Secant (sec)
• Cosecant (csc)
• Cotangent (cot)

If we have the exact value of any one trigonometric function for a degree then we can find the other function for the same degree as follow.

sin 300° = sin (-60 + 360)° = sin (-60) = - sin 60 =
`-(√(3))/(2)`

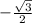
cos 300° = cos (-60 + 360)° = cos (-60) = cos 60 =
`(1)/(2)`

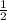
tan 300° =
`(\sin 300^(\circ))/(\cos 300^(\circ))=(-(√(3))/(2))/((1)/(2))=-√(3)`

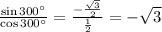
cot 300° =
`(1)/(\tan 300^(\circ))=(1)/(-√(3))=-(1)/(√(3))=-(√(3))/(3)`

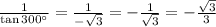
sec 300° =
`(1)/(\cos 300^(\circ))=(1)/((1)/(2))=2`

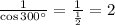
csc 300° =
`(1)/(\sin 300^(\circ))=(1)/(-(√(3))/(2))=-(2)/(√(3))=-(2√(3))/(3)`

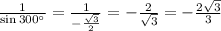
Note : sin (-x) = -sin x and cos (-x) = cos x