Answer:
Step-by-step explanation:
Given
Car at point A and E are travelling along circular path with same radius
Car at point A has twice the velocity of car at Point B
Assuming the magnitude of velocity constant
Let r be the radius of circle and v the be velocity of car at point B
there will only be centripetal acceleration and no tangential acceleration
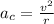
at Point A
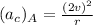
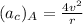
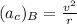
so the magnitude of acceleration of car at point A is more than magnitude of car at Point B