Question

Going down the river went 18km/h. Going up the river it only went 4km/h. Find the speed of the boat in still water and the speed of the current.

Answer 1

The speed of boat in still water is 11 km/h

The speed of current is 7 km/h

Explanation:

Given as :

The speed in downstream = 18 km/h

The speed in upstream = 4 km/h

Let The speed of boat in still water = x km/h

Let The speed of current = y km/h

Now, According to question

∵ downstream speed = 18

So, x + y = 18 km/h .........A

∵ upstream speed = 4

So, x - y = 4 km/h ..........B

Now, Solving equation A and B

(x + y) + (x - y) = 18 + 4

Or, (x + x) + (y - y) = 22

Or, 2 x + 0 = 22

∴ x =
`(22)/(2)`

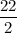
i.e x = 11 km/h

So, The speed of boat = x = 11 km/h

Now, Put The value of x into eq A

∵ x + y = 18

Or, 11 + y = 18

∴ y = 18 - 11

i.e y = 7 km/h

So, The speed of current = y = 7 km/h

Hence,The speed of boat in still water is 11 km/h and The speed of current is 7 km/h . Answer