Question

Which of the following can best be evaluated using the half-angle formula for the sine function?

a. sin (1/2 cos^-1(-2))
b. sin (tan^-1(1) + cos^-1(sqrt 3/2))
c. sin (1/2 cos^-1 (-2/3))
d. sin (cos^-1(-1/2))

Answer 1

c)
`sin((1)/(2) cos^(-1)(-(2)/(3)))`

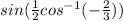
Explanation:

Option a) cannot be solved because there is no such thing as
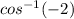`cos^(-1)(-2)` since the
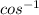`cos^(-1)` function can only be used with values between -1 and 1 due to its domain. So option a is not valid.

Option b) would be better solved by directly calculating the given functions since the numbers used there are know and would give regular angles as answers, so the half-angle formula would not be too practical here.

Option d) would also be better solved by directly calculating the given function, since -1/2 is a known value and would return a known angle as an answer.

So the best candidate to use the half-angle formula would be option b, which would be solved like this:

The half-angle formula is the following:

`sin((\theta)/(2))=\pm \sqrt{(1-cos \theta)/(2)}`

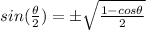
so in this case:

`(\theta)/(2)=(cos^(-1)(-(2)/(3)))/(2)`

which means that:

`\theta = cos^(-1)(-(2)/(3))`

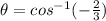
which yields:

`sin((1)/(2) cos^(-1)(-(2)/(3))) =\pm \sqrt{(1-cos (cos^(-1)(-(2)/(3))))/(2)}`

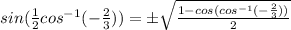
This can now be simplified so we get:

`sin((1)/(2) cos^(-1)(-(2)/(3))) =\pm \sqrt{(1+(2)/(3))/(2)}`

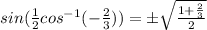
this can be further simplified to:

`sin((1)/(2) cos^(-1)(-(2)/(3))) =\pm \sqrt{(5)/(6)}`

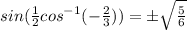
when rationalized we get:

`sin((1)/(2) cos^(-1)(-(2)/(3))) =\pm (√(30))/(6)`

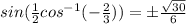
the sign of the final answer will depend on the quadrant the angle is located at.