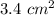Question

If a = 2 cm and r = 3.4 cm, find the area of the regular pentagon.

Round the answer to one decimal place.
Area =
cm

Answer 1

`Area = 3.4\ cm^(2)`

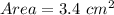
Explanation:

Assume a pentagon has equal length where a be the side of the pentagon and r be the apothem of the pentagon.

Given:

Sides of pentagon
`a=2\ cm`

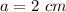
apothem of pentagon
`r=3.4\ cm`

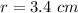
The area of the pentagon formula is given below.

`A = (1)/(2)* bh`

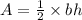
Where b = length of the base or side

And h = height of apothem

Now, we substitute side and apothem length in above formula.

`A = (1)/(2)* 2* 3.4`

`A = 3.4\ cm^(2)`

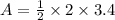
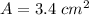
Therefore, the area of the pentagon is
`3.4\ cm^(2)`