Question

You have dimes and quarters in your pocket. There are 12 coins that total $2.25. Write and solve a system of linear equations to find the number of dimes and the number of quarters

Answer 1

Hence the System of equation are
`\left \{ {{x+y=12} \atop {0.1x+0.25y=2.25}} \right.`

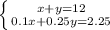
There are 5 dimes and 7 quarters in my pocket.

Explanation:

Let Number of dimes be 'x'.

Also Number of quarters be 'y'.

Now Given:

Total Number of Coins = 12

So the equation can be framed as;

`x+y=12 \ \ \ \ equation \ 1`

Also Given:

Total Amount in pocket = $2.25

Now we know that 1 dime = $0.1

Also 1 quarter =$0.25

So the equation can be framed as;

`0.1x+0.25y = 2.25 \ \ \ \ equation \ 2`

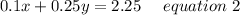
Hence the System of equation are
`\left \{ {{x+y=12} \atop {0.1x+0.25y=2.25}} \right.`

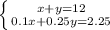
Now Solving the equation we get;

Now Multiplying equation 2 by 10 we get;

`10(0.1x+0.25y)=2.25*10\\\\10*0.1x+10*0.25y=22.5\\\\x+2.5y=22.5 \ \ \ \ equation\ 3`

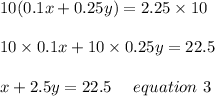
Now Subtracting equation 1 from equation 3 we get;

`(x+2.5y)-(x+y)=22.5-12\\\\x+2.5y-x-y =10.5\\\\1.5y =10.5\\\\y= (10.5)/(1.5)= 7`

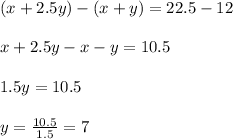
Now Substituting the value of y in equation 1 we get;

`x+y=12\\\\x+7=12\\\\x=12-7 =5`

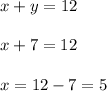
Hence there are 5 dimes and 7 quarters in my pocket.