Answer:
Explanation:
We are to find gcd of a and b using linear combination algorithm
a) 7 and 11. 1= 3(7)-2(11). Hence GCD =1
b) -28 and -63:
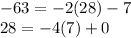
7=-2(-28)+(-63)
So 7 is GCD
c)
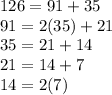
So 7 is GCD and 7 = 7(91)-5(126)
d) 630 and 132
GCD is 6.
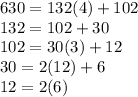
6=630(-9)+43(132)
e) 7245 and 4784
GCD is 23
23 = 7245(35)+4784(-53)
f) 6499 and 4288
GCD is 67
67 = 6499(-31)+4288(47)