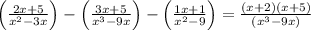Question

What is the difference?

Answer 1

Option b) is correct.

The difference of given expression is

`\left((2x+5)/(x^2-3x)\right)-\left((3x+5)/(x^3-9x)\right)-\left((1x+1)/(x^2-9)\right)=((x+2)(x+5))/((x^3-9x))`

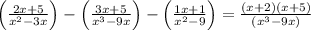
Explanation:

Given expression is

`\left((2x+5)/(x^2-3x)\right)-\left((3x+5)/(x^3-9x)\right)-\left((1x+1)/(x^2-9)\right)`

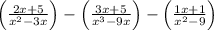
To find their difference

`\left((2x+5)/(x^2-3x)\right)-\left((3x+5)/(x^3-9x)\right)-\left((x+1)/(x^2-9)\right)`

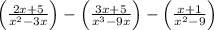
The expression can be written as below

`\left((2x+5)/(x^2-3x)\right)-\left((3x+5)/(x^3-9x)\right)-\left((x+1)/(x^2-9)\right)=\left((2x+5)/(x (x-3))\right)-\left((3x+5)/(x(x^2-9))\right)-\left((x+1)/(x^2-9)\right)`

`=\left((2x+5)/(x(x-3))\right)-\left((3x+5)/(x(x^2-3^2))\right)-\left((x+1)/(x^2-3^2)\right)`

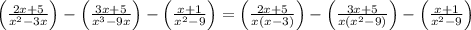
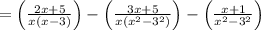
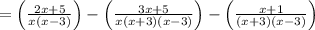`=\left((2x+5)/(x(x-3))\right)-\left((3x+5)/(x(x+3)(x-3))\right)-\left((x+1)/((x+3)(x-3))\right)` (using
`a^2-b^2=(a+b)(a-b)`)

`=((2x+5)(x+3)-(3x+5)-(x+1)x)/(x(x+3)(x-3))`

`=(2x^2+6x+5x+15-3x-5-x^2-x)/(x(x+3)(x-3))`

`=(x^2+7x+10)/(x(x+3)(x-3))`

`=((x+2)(x+5))/(x(x+3)(x-3))`

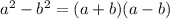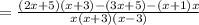
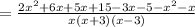
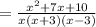
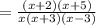
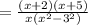`=((x+2)(x+5))/(x(x^2-3^2))` (using
`a^2-b^2=(a+b)(a-b)`)

`=((x+2)(x+5))/(x(x^2-9))`

`=((x+2)(x+5))/((x^3-9x))`

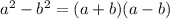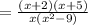
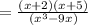
Therefore
`\left((2x+5)/(x^2-3x)\right)-\left((3x+5)/(x^3-9x)\right)-\left((1x+1)/(x^2-9)\right)=((x+2)(x+5))/((x^3-9x))`

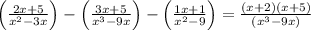
Option b) is correct.

The difference of given expression is

`\left((2x+5)/(x^2-3x)\right)-\left((3x+5)/(x^3-9x)\right)-\left((1x+1)/(x^2-9)\right)=((x+2)(x+5))/((x^3-9x))`