Question

Lizzie has 30 coins that total $4.80. All of her coins are dimes, D, and quarters, Q. Algebraically determine how many of each type of coin did Lizzie have?

Answer 1

Lizzie has 18 dimes and 12 quarters

Solution:

Let "d" be the number of dimes

Let "q" be the number of quarters

We know that,

value of 1 dime = $ 0.10

value of 1 quarter = $ 0.25

Given that LIzzie has 30 coins

number of dimes + number of quarters = 30

d + q = 30 ---- eqn 1

Also given that the coins total $ 4.80

number of dimes x value of 1 dime + number of quarters x value of 1 quarter = 4.80

`d * 0.10 + q * 0.25 = 4.80`

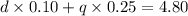
0.1d + 0.25q = 4.8 ------ eqn 2

Let us solve eqn 1 and eqn 2

From eqn 1,

d = 30 - q ---- eqn 3

Substitute eqn 3 in eqn 2

0.1(30 - q) + 0.25q = 4.8

3 - 0.1q + 0.25q = 4.8

0.15q = 1.8

q = 12

From eqn 3,

d = 30 - 12

d = 18

Thus she has 18 dimes and 12 quarters