Question

Find the inverse of f(x)=6/5x-3

Answer 1

For this case we must find the inverse of the following function:

`f (x) = \frac {6} {5} x-3`

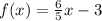
We change
`f (x)` by y:

`y = \frac {6} {5} x-3`

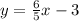
We exchange the variables:

`x = \frac {6} {5} y-3`

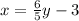
We clear the variable "y":

We add 3 to both sides of the equation:

`x + 3 = \frac {6} {5} y`

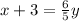
We multiply by 5 on both sides of the equation:

`5x + 15 = 6y`

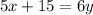
We divide between 6 on both sides of the equation:

`y = \frac {5x + 15} {6}`

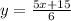
We simplify:

`y = \frac {5x} {6} + \frac {15} {6}\\y = \frac {5x} {6} + \frac {5} {2}`

We change y for
`f^( - 1) (x)`:

`f ^ {- 1 }(x) = \frac {5x} {6} + \frac {5} {2}`

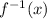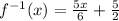
Finally, the inverse function is:

`f ^ {- 1} (x) = \frac {5x} {6} + \frac {5} {2}`

Answer:

`f ^ {- 1} (x) = \frac {5x} {6} + \frac {5} {2}`