Answer:
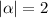
Explanation:
Since
 and
and
 are complex conjugates, let's define them as follows:
are complex conjugates, let's define them as follows:
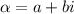
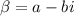
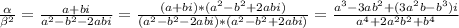
Since
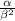 is a real number, complex part of above result must be zero.
is a real number, complex part of above result must be zero.
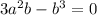
From to hold above equality,
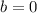 or
or
 .
.
However, since
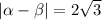 ,
,
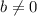
So,
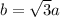 or
or
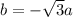
And since
 and
and
 are complex conjugates, taking plus or minus sign as found above will not affect the result, so let's write the last version of
are complex conjugates, taking plus or minus sign as found above will not affect the result, so let's write the last version of
 and
and
 as follows:
as follows:

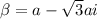
Since
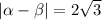
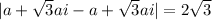 ⇒
⇒
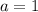
Finally,
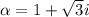 ⇒
⇒
