Question

Please answer all correctly !!

Answer 1

See below for answers and explanations

Explanation:

Problem 1

To convert from polar to Cartesian coordinates, recall that
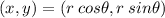`(x,y)=(r\:cos\theta,r\:sin\theta)`, thus,
`(x,y)=(6\:cos(5\pi)/(6),6sin(5\pi)/(6))=(6(-(√(3))/(2)),6((1)/(2)))=(-3√(3),3)`

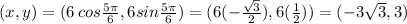
Therefore, C is the correct answer

Problem 2

Convert from polar to Cartesian coordinates:

`(x,y)=(-5\:cos(2\pi)/(3),-5\:sin(2\pi)/(3))=(-5(-(1)/(2)),-5((√(3))/(2)))=((5)/(2),(-5√(3))/(2))`

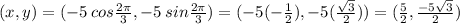
Therefore, U is the correct answer

Problem 3

Since
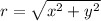`r=√(x^2+y^2)`, then
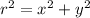`r^2=x^2+y^2`. Don't also forget to use the substitution
`x=r\:cos\theta`:

`x^2+y^2-7x=0\\\\r^2-7rcos\theta=0\\\\r(r-7cos\theta)=0\\\\r-7cos\theta=0\\\\r=7cos\theta`

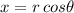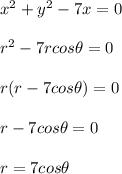
Therefore, B is the correct answer

Problem 4

`r=(tan\theta)(sec\theta)\\\\r=((sin\theta)/(cos\theta))((1)/(cos\theta))\\ \\(r^2)/(r)=((rsin\theta)/(rcos\theta))((r)/(rcos\theta))\\ \\(x^2+y^2)/(√(x^2+y^2))=((y)/(x))((√(x^2+y^2))/(x))\\ \\x^2+y^2=(y(x^2+y^2))/(x^2)\\ \\1=(y)/(x^2)\\\\x^2=y`

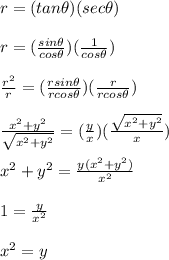
Therefore, A is the correct answer