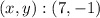For this case we have the following system of equations:
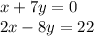
According to the first equation we have:
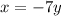
Thus, we have the equivalent system:
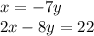
Substituting the first equation in the second equation we have:
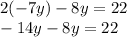
Equal signs are added and the same sign is placed:
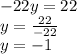
We look for the value of the variable x:
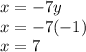
Thus, the system solution is:
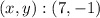
Answer: