The slope of line is
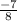
The point slope form is found when point (7, -4) is used is
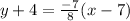
The slope intercept form is
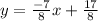
Solution:
We have to find the equation of the line that passes through the points 7, -4 and -1, 3
Point slope form:
The point slope form is given as:
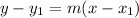
Where "m" is the slope of line
Given two points are (7, -4) and (-1, 3)
Let us find the slope of line
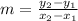
Substituting
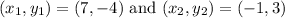
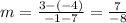
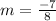
Thus slope of line is found
Substitute value of m and point (7, -4) in eqn 1
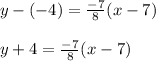
Thus the point slope form is found when point (7, -4) is used
Slope intercept form:
The slope intercept form is given as:
y = mx + c ----- eqn 1
Where "m" is the slope of line and "c" is the y - intercept
Substitute m = -7/8 and (x, y) = (7, -4) in eqn 1
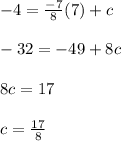
Substitute m = -7/8 and
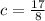 in eqn 1
in eqn 1
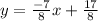
Thus the required equation of line is found