Answer:
The largest value is 99,997
Explanation:
We can see the congruence of the expression module 5 according to the congruence of n module 5. First, we simplify the expression module 5. 8 is replaced by 3, 14 n can be replaced by 4n (10n is 0 module 5), and -24 is replaced by 1. With this, the expression is congruent module 5 to the following one
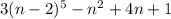
Also, due to Fermat Theorem, if n-2 is not a multiple of 5, then (n-2)⁴ is congruent to 1 module 5. In any case, (n-2)⁵ is congruent to (n-2) module 5 (even if n-2 is a multiple of 5). So we can replace (n-2)⁵ with (n-2) in the expression.
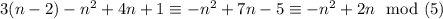
Now, lets see the congruences
- n congruent to 0 module 5:

- n congruent to 1 module 5:
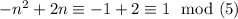
- n congruent to 2 module 5:
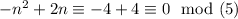
- n congruent to 3 module 5:
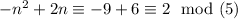
- n congruent to 4 module 5:

So, only for 0 and 2 the expression is a multiple of 5. As a result, the largest value less than 100,000 that is a multiple of 5 is 99,997, obtained by picking the largest number less than 100,000 that is either congruent to 0 or congruent to 2 module 5.