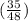Question

Bert didn't finish 1/8 of the problems on a math test he made Mistakes on 1/6 of the problems the rest he answered correctly what fraction of the problems did he answer correctly

Answer 1

The fraction of the problems did he answer correctly is
`((35)/(48))`

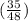
Explanation:

Here, let us assume the total number of problems in the test = p

Now, Bert did not finish 1/8 of the problems.

⇒The number of unfinished problems by Bert =
`(1)/(8)  * p= (p)/(8)`

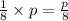
Also, the number of finished problems

= Total problems - Unfinished problems

`= p - (p)/(8)  = (7p)/(8)`

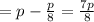
Now, again 1/6 of the total finished problems had mistakes.

So, the number of problems with mistakes =
`(1)/(6)  * (7p)/(8)   = (7p)/(48)`

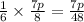
The total answers did correctly

= Total answers done - Problem with mistakes

`= (7p)/(8) - (7p)/(48)  = ((42 - 7)p)/(48)   = (35)/(48)p`

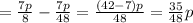
Hence, the fraction of the problems did he answer correctly is
`((35)/(48))`