Question

Plz help super fast 4 mins

Answer 1

A. 10%

Explanation:

Let events A nad B be:

A = an employee is a female

B = an employee is under the age of 30.

Use formula

`P(A\cup B)=P(A)+P(B)-P(A\cap B)`

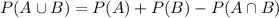
There are 200 employees, 150 of them are female, then

`P(A)=(150)/(200)=(3)/(4)=0.75`

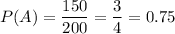
There are 200 employees, 40 of them are under the age of 30, then

`P(B)=(40)/(200)=(1)/(5)=0.2`

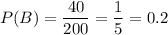
The probability of randomly selecting an employee who is a female or under the age of 30 is 85%, then

`P(A\cup B)=0.85`

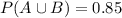
Thus,

`0.85=0.75+0.2-P(A\cap B)\\ \\0.85=0.95-P(A\cap B)\\ \\P(A\cap B)=0.95-0.85=0.1`

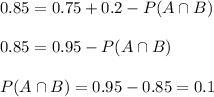
Therefore, the probability of randomly selecting an employee who is a female and under the age of 30 is 0.1 or 10%.