Question

Determine whether the degree of the function is even or odd and whether the function itself is even or odd.

Answer 1

There are Even, Odd and None of them and this does not depend on the degree but on the relation. An Even function:
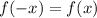`f(-x)=f(x)` And Odd one:
`-f(x)=f(-x)`

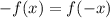
Explanation:

1) Firstly let's remember the definition of Even and Odd function.

An Even function satisfies this relation:

`f(-x)=f(x)`

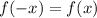
An Odd function satisfies that:

`-f(x)=f(-x)`

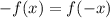
2) Since no function has been given. let's choose some nonlinear functions and test with respect to their degree:

`f(x)=x^(2)-4, g(x)= x^(5)+x^(3)`

`f(x)=x^2 -4\Rightarrow f(-x)=(-x)^(2)-4\Rightarrow f(-x)=x^(2)-4\therefore f(x)=f(-x)`

`g(-x)=-(x^(5)+x^(3))\Rightarrow g(-x)=-x^(5)-x^(3)\Rightarrow g(-x)=-g(x)`

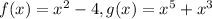
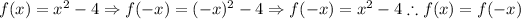
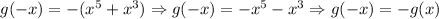
3) Then these functions are respectively even and odd, because they passed on the test for even and odd functions namely,
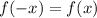`f(-x)=f(x)` and
`-f(x)=f(x)` for odd functions.

Since we need to have symmetry to y axis to Even functions, and Symmetry to Odd functions, and moreover, there are cases of not even or odd functions we must test each one case by case.