Answer:
c. Will produce a slope field with rows of parallel tangents
Explanation:
We can write a differential equation that is a function of y only as:
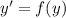
So the derivative, in this particular case, of any function will be a function of the dependent variable y only, it means that the curves you will get should all be pointing in the same direction for each value of x. Therefore the sketch of the slopes field would have parallel curves for each value of x, in other words, it will produce a slope field with rows of parallel tangents.
I hope it helps you!