Question

M m< B = 80 + x

m< C=110 - 3x
m Quadrilateral ABCD is a parallelogram if both pairs of opposite angles are equal. Prove that Quadrilateral ABCD is
a parallelogram by finding the value of x.

Answer 1

`x=5`

Explanation:

The complete question is

m ∠ A = 100 - x

m ∠ B = 80 + x

m ∠ C = 110 - 3x

m ∠ D = 75 + 2x

Quadrilateral ABCD is a parallelogram if both pairs of opposite angles are equal. Prove that Quadrilateral ABCD is a parallelogram by finding the value of x.

Options

A) x = 5

B) x = 7

C) x = 10

D) x = 15/2

we know that

In a parallelogram, opposite angles are parallel and consecutive angles are supplementary

so

m ∠ A=m ∠ C

m ∠ B=m ∠ D

m ∠ A+m ∠ B=180°

m ∠ B+m ∠ C=180°

step 1

Find the value of x

we know that

m ∠ A=m ∠ C

substitute the given values

`(100-x)^o=(110-3x)^o`

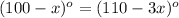
solve for x

Group terms

`3x-x=110-100`

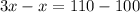
Combine like terms

`2x=10`

`x=5`

step 2

Verify the measure of the angles

`m\angle A=100-5=95^o`

`m\angle B=80+5=85^o`

`m\angle C=110-3(5)=95^o`

`m\angle D=75+2(5)=85^o`

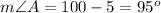
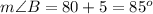
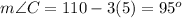
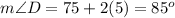
therefore

`m\angle A=m\angle C` ---> is ok

`m\angle B=m\angle D` ---> is ok

`m\angle A+m\angle B=180^o` ---> is ok

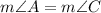`m\angle B+m\angle C=180^o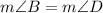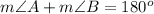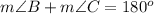` ---> is ok