Answer:
The first is a solution, but the second is not
Explanation:
we know that
If a ordered pair is a solution of a linear equation, then the ordered pair must satisfy the linear equation (makes the equation true)
we have
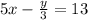
Verify the first ordered pair
Part a) we have (2,-9)
For x=2, y=-9
substitute in the linear equation
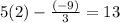
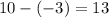
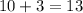
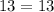 ----> is true
----> is true
so
The ordered pair satisfy the equation
The ordered pair is a solution of the equation
Verify the second ordered pair
Part b) we have (3,-6)
For x=3, y=-6
substitute in the linear equation
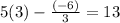
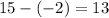
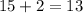
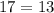 ----> is not true
----> is not true
so
The ordered pair not satisfy the equation
The ordered pair is not a solution of the equation