Question

An airplane takes 3 hours to travel a distance of 2250 miles with the wind. The return trip takes 5 hours against the wind. Find the speed of the plane in still air and the speed of the wind.

Answer 1

Speed of Plane = 600 miles per hour

Speed of Wind = 150 miles per hour

Explanation:

The distance equation is D = RT

Where

D is the distance

R is the rate

T is the time

Let rate of airplane be "x" and rate of wind be "c"

Also, note: rate with wind is airplane's and wind's, so that would be "x + c"

and rate against the wind is airplane's minus the wind's, so that would be "x - c"

Now,

2250 miles with wind takes 3 hours, so we can write:

D = RT

2250 = (x + c)(3)

and

2250 miles against the wind takes 5 hours, we can write:

D = RT

2250 = (x - c)(5)

Simplifying 1st equation:

`2250 = (x + c)(3)\\3x+3c=2250`

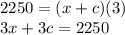
Simplifying 2nd equation:

`2250 = (x - c)(5)\\5x -5c=2250`

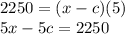
Multiplying the 1st equation by 5, gives us:

`5*[3x+3c]=2250\\15x+15c=11250`

Multiplying the 2nd equation by 3 gives us:

`3*[5x -5c=2250]\\15x-15c=6750`

Adding up these 2 equations, we solve for x. Shown below:

`15x+15c=11250\\15x-15c=6750\\---------\\30x=18000\\x=600`

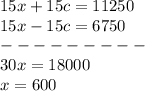
Now putting this value of x into original 1st equation, we solve for c:

`3x+3c=2250\\3(600)+3c=2250\\1800+3c=2250\\3c=450\\c=150`

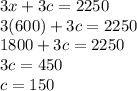
Speed of Plane = 600 miles per hour

Speed of Wind = 150 miles per hour