Question

A Gardner plants two trees

Type A is 9 feet tall and grows a rate of 17 inches per year
Type b is 2 feet tall and grows a rate of 24 in per year
Algebraically determine exactly how many years it will take for these trees to be the same height

Answer 1

After 12 yrs the height of both trees type A and type B will be same.

Explanation:

Given,

Height of Type A at the time of planting =
`9\ ft=9*12=108\ in`

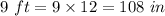
Height of Type B at the time of planting =
`2\ ft=2*12=24\ in`

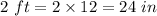
Let the number of years be 'x'.

After 'x' years height of Type A =
`108+17x`

After 'x' years height of Type B =
`24+24x`

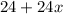
We have to find out the number of years will take for these trees to be the same height.

Now according to question, after 'x' years the height of plant type A and plant type B will be equal.

`108+17x=24+24x`

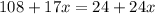
Combining the like terms, we get;

`24x-17x=108-24\\\\7x=84\\\\x=(84)/(7)=12\ yrs`

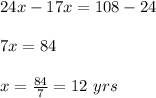
Hence After 12 yrs the height of both trees type A and type B will be same.