Answer:
The maximum value of P is 34 and the minimum value of P is 0
Explanation:
we have the following constraints
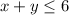 ----> constraint A
----> constraint A
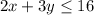 ----> constraint B
----> constraint B
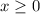 ----> constraint C
----> constraint C
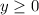 ----> constraint D
----> constraint D
Solve the feasible region by graphing
Using a graphing tool
The vertices of the feasible region are
(0,0),(0,5.33),(2,4),(6,0)
see the attached figure
To find out the maximum and minimum value of the objective function P, substitute the value of x and the value of y for each of the vertices in the objective function P, and then compare the results
we have
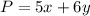
For (0,0) ---->
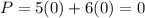
For (0,5.33) ---->
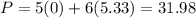
For (2,4) ---->

For (6,0) ---->
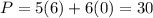
therefore
The maximum value of P is 34 and the minimum value of P is 0