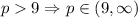Answer:
(i)
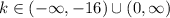
(ii)
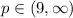
Explanation:
(i) Given equation
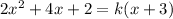
Rewrite this equation as quadratic equation in the standard form:
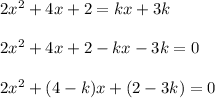
If the equation has two distinct real roots, then its discriminant is greater than 0. Find the discriminant:
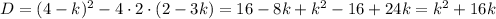
Solve the inequality
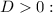
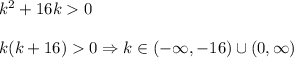
(ii) The quadratic expression is always greater than 0 when:
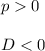
Find the discriminant:
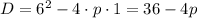
Solve the inequality
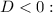
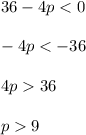
Assuming that
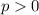 and
and
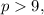 you get
you get