Answer:
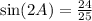
Explanation:
Double angle identity for sine is
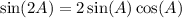 .
.
We know
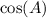 . We now need to find
. We now need to find
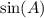 to find our answer.
to find our answer.
Recall the following
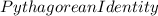 :
:
 .
.
Replace
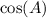 with
with
 :
:
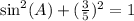
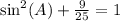
Subtract
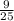 on both sides:
on both sides:
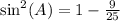

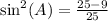

Now to finally get the value of
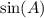 take the square of both sides:
take the square of both sides:
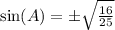
Since
 is in the interval
is in the interval
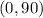 , then
, then
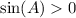 .
.
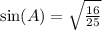
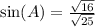

So let's finally find the numerical value of
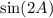 .
.
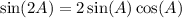
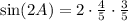
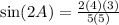
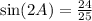
Side note:
If
 is between 0 and 90 degrees, then we are in the first quadrant.
is between 0 and 90 degrees, then we are in the first quadrant.
If we are in the first quadrant, both
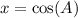 and
and
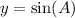 are positive.
are positive.