Question

An equation is shown below: 4(2x − 3) = 4 Part A: What is the solution to the equation above? Show your work using inverse operations. (5 points) Part B: Check using substitution to make sure your answer is correct. (5 points)

Answer 1

see explanation

Explanation:

(A) Given

4(2x - 3) = 4 ( divide both sides by 4 )

2x - 3 = 1 ( add 3 to both sides )

2x = 4 ( divide both sides by 2 )

x = 2

(B)

As a check substitute x = 2 into the left side of the equation and if equal to the right side then it is the solution.

4(2(2) - 3) = 4(4 - 3) = 4(1) = 4 = right side

Hence x = 2 is the solution

Answer 2

The solution of the given equation is x = 2.

Explanation:

The given linear equation is,

`4(2x-3)=4`

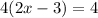
At first, we will eliminate '4' from the LHS by dividing both sides i.e., LHS and RHS by 4 because '4' is present in multiplication with the term containing unknown in LHS.

So, dividing both sides by '4', we get

`(4(2x-3))/(4) = (4)/(4)`

`\implies 2x - 3 = 1`

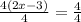
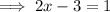
Our next step will be to eliminate '3' from the LHS that is being subtracted from the term containg unknown variable. For this, we will add '3' on both sides of the above obtained equation.

So, adding '3' on both sides, we get

`2x - 3 + 3 = 1 + 3`

`\implies 2x = 4`

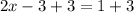
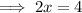
Now, we will eliminate '2' from the LHS that is in multiplication with the unknown variable 'x'.

For this, we will divide both sides of the above obtained equation by '2'.

So, dividing both sides by '2', we get

`(2x)/(2)=(4)/(2)`

`\implies x = 2`

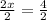
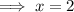
CHECKING :

For this, we will substitute x = 2 in the LHS of the given equation and then check whether it is equal to RHS or not.

LHS = 4(2x - 3)

= 4(2 × 2 - 3)

= 4(4 - 3)

= 4 × 1

= 4

= RHS

So, the solution of the given equation is x = 2.