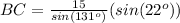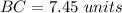Answer:

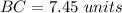
Explanation:
see the attached figure to better understand the problem
Remember that in a parallelogram opposites sides are parallel and congruent, opposites angles are congruent and consecutive angles are supplementary
step 1
Find the measure of angle ACB
we have
 ----> given problem
----> given problem
 ----> by alternate interior angles
----> by alternate interior angles
 ----> given problem
----> given problem
so
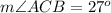
step 2
Find the measure of angle ABC
The sum of the interior angles in any triangle must be equal to 180 degrees
In the triangle ABC of the figure
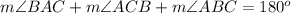
substitute the given values
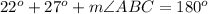
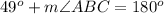
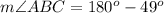
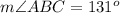
step 3
Find the length side AB
In the triangle ABC
Applying the law of sines
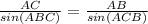
substitute the given values
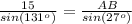
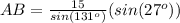

step 4
Find the length side BC
In the triangle ABC
Applying the law of sines

substitute the given values