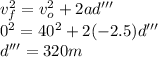Answer:
5 m
80 m
320 m
Step-by-step explanation:
 = Initial speed of the car = 10 ms⁻¹
= Initial speed of the car = 10 ms⁻¹
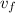 = Final speed of the car = 0 ms⁻¹
= Final speed of the car = 0 ms⁻¹
 = Stopping distance of the car = 20 m
= Stopping distance of the car = 20 m
 = acceleration of the car
= acceleration of the car
On the basis of above data, we can use the kinematics equation
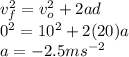
 = Initial speed of the car = 5 ms⁻¹
= Initial speed of the car = 5 ms⁻¹
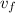 = Final speed of the car = 0 ms⁻¹
= Final speed of the car = 0 ms⁻¹
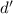 = Stopping distance of the car
= Stopping distance of the car
 = acceleration of the car = - 2.5 ms⁻²
= acceleration of the car = - 2.5 ms⁻²
On the basis of above data, we can use the kinematics equation

 = Initial speed of the car = 20 ms⁻¹
= Initial speed of the car = 20 ms⁻¹
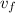 = Final speed of the car = 0 ms⁻¹
= Final speed of the car = 0 ms⁻¹
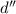 = Stopping distance of the car
= Stopping distance of the car
 = acceleration of the car = - 2.5 ms⁻²
= acceleration of the car = - 2.5 ms⁻²
On the basis of above data, we can use the kinematics equation

 = Initial speed of the car = 40 ms⁻¹
= Initial speed of the car = 40 ms⁻¹
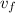 = Final speed of the car = 0 ms⁻¹
= Final speed of the car = 0 ms⁻¹
 = Stopping distance of the car
= Stopping distance of the car
 = acceleration of the car = - 2.5 ms⁻²
= acceleration of the car = - 2.5 ms⁻²
On the basis of above data, we can use the kinematics equation