Question

A differential equation of the form y prime (t )equals​F(y) is said to be autonomous​ (the function F depends only on​ y). The constant function yequals y 0 is an equilibrium solution of the equation provided Upper F (y 0 )equals0 ​(because then y prime (t )equals​0, and the solution remains constant for all​ t). Note that equilibrium solutions correspond to horizontal line segments in the direction field. Note also that for autonomous​ equations, the direction field is independent of t. Consider the equation y prime (t )equals3 sine y .

a. Find all equilibrium solutions in the interva

Answer 1

y=n*pi, where n is an integer.

Explanation:

We have the equation:

`y'(t)=3sin(y)`

Which is autonomous because the independent variable does not appear explicitly.

Now, we are asked about all the equilibrium solutions for such autonomous equation. Let's remember that the solution equilibrium y=y0 when F(y0)=0.

Then, matching the given equation to zero, we have:

`y'(t)=3sin(y)=0`

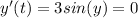
Which is fulfilled when the sine function has a value of zero. The sine function is worth zero in y=n*pi where n is an integer.