Question

The marginal cost of manufacturing an item when x thousand items are produced is dC/dx= 4x^3 - 6x + 5 dolars/item.Find the cost function C(x) if C(0)=550

Answer 1

The cost function is
`C(x)=x^4-3x^2+5x+550`.

Explanation:

It is given that the marginal cost of manufacturing an item when x thousand items are produced is

`(dC)/(dx)=4x^3-6x+5`

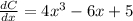
We need to find the cost function.

Multiply both sides by dx.

`dC=(4x^3-6x+5)dx`

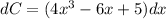
Integrate both sides to find the cost function.

`\int dC=\int (4x^3-6x+5)dx`

`\int dC=4\int x^3dx-6\int xdx+5\int 1 dx`

`C(x)=4((x^4)/(4))-6((x^2)/(2))+5x+C`

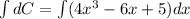
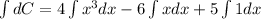
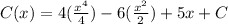
where, C(x) is const function and C is a constant.

`C(x)=x^4-3x^2+5x+C`

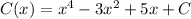
It is given that C(0)=550. Substitute x=0 in the above function.

`C(0)=(0)^4-3(0)^2+5(0)+C`

`C(0)=C`

`550=C`

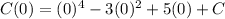
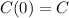
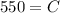
Therefore, the cost function is
`C(x)=x^4-3x^2+5x+550`.