Question

In a figure, OB is the radius of a big semicircle and XB is the radius of the small semicircle. Given that OX = 14 cm, Calculate the area and the perimeter of the shaded region in the figure.

(Take π = 22/7).

Answer 1

perimeter of the shaded region = 88 +44+28 =160 cm

Explanation:

perimeter of shaded region = length AO + arc OB + arc AB

length AO = radius of bigger circle

radius of bigger circle = OX + OB = 2×radius of smaller circle = 2×14 cm = 28 cm

therefore AO = 28 cm

length of arc oB= half of circumference of smaller circle =
`\pi`×14 = 44 cm

length of arc ab = half of circumference of bigger circle =
`\pi`×28 =
`(22)/(7)`×28= 88

therefore perimeter of the shaded region = 88 +44+28 =160 cm

area of the shaded region = half of area of bigger circle - half of area of smaller circle

=
`(1)/(2) \pi 28^(2) -(1)/(2) \pi 14^(2)`

=
`(\pi )/(2) (28^(2) -14^(2) )`

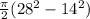
solving we gen area of shaded region = 924