Question

The value of y varies inversely as the square of x, and y=4, when x=3.

Find the value of x when y=9

Answer 1

The value of x when y = 9 is x = 2 or x = -2

Solution:

Given that value of y varies inversely as the square of x, and y=4, when x=3.

Therefore the initial statement is:

`y \propto (1)/(x^(2))`

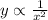
To convert to an equation, multiply by k, the constant of variation

`y = k * (1)/(x^2)`

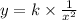
`y = (k)/(x^2)` --- eqn 1

Given that,

y = 4 when x = 3

Now find value of k

`4 = (k)/(3^2)\\\\4 * 9 = k\\\\k = 36`

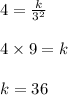
Find the value of x when y = 9

x = ?

y = 9

From eqn 1,

`9 = (k)/(x^2)\\\\9 = (36)/(x^2)\\\\x^2 = 4\\\\x = \pm 2`

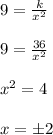
Thus value of x is found