Question

15 points!! Please help! please explain how you got you answers

Answer 1

We observe that a line will pass through 3 points, but to find a slope we only need two.

We see that it passes through points (assuming the scale of graph is 1 : 1)
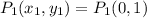`P_1(x_1,y_1)=P_1(0,1)` and
`P_2(x_2,y_2)=P_2(2,-1)`.

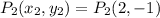We can use slope formula that applies for any line and produce the same slope for any two different points on the line

`m=\frac{\Delta{y}}{\Delta{x}}=(y_2-y_1)/(x_2-x_1)=(-1-1)/(2-0)=-1`

So the slope is -1 also it intersects y-axis at
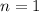`n=1` so the general form of the linear function is

`f(x)=mx+n`

That is in your case

`\boxed{f(x)=-x+1}`

Hope this helps.