Answer:
n = 1
Explanation:
First, rearrange the equation to standard form 0 = ax² + bx + c, when everything equals 0.
5n² = 5
5n² - 5 = 0
State the variables a, b and c.
a = 5; b = 0; c = -5
Substitute a, b, and c into the quadratic formula.
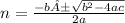
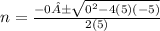 Substitute
Substitute
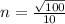 Simplify inside the √ and bottom
Simplify inside the √ and bottom
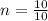 Simplify the top
Simplify the top
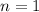 Final answer
Final answer
Therefore the solution is n = 1.
The quadratic formula usually is written with x, but it can be solved with any variable in standard form.