Answer:
Undefined
Explanation:
1. In order to even begin to answer this question, we'll need to find the definition of a few terms:
Coefficient: A constant quantity placed before a variable in an equation.
- ex: the 3 in the expression 3x^3 is the coefficient.
The expansion of an equation is the unfactored version of an equation.
- ex: x^2 +2x + 1 is the expansion of (x + 1)^2
2. Based on these definitions, the question is asking:
"What number is in front of of x^3 in the expanded version of (6x + 5y)^4?"
It still sounds super confusing, but at least its comprehensible.
3. Now that we know what we're being asked for, we can begin to solve... but how? Expanding (6x + 5y)^4 seems like it would take forever right?
This is when it gets complicated. You'll to have a couple concepts in your mind:
- The equation
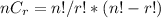 . This is called the Combination Formula
. This is called the Combination Formula - Pascal's Triangle. I recommend finding an image of it.
If what I'm doing right now seems confusing, look up how to, "Find the Coefficient of an Expansion." I checked and there are videos on this.
4. Here is the order of how we solve this problem from this point forward:
- Define our variables
- Translate our variables into the format that our question is asking for.
- Plug the translated variable into the Combination Formula.
- Solve
5. We are given two different variables to expand. (6x) and (5y). The question is asking for the coefficient in front of x^3, so our format is (6x)^3(5y)^0. The 5y should still be shown although its exponent is 0.
I'm going to have to again stress looking for videos on what exactly I'm doing. I'm sorry that I can't properly teach Combinations. From this point on you may have trouble understanding what's going on.
Math:
- (6x)^3(5y)^0
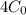 (6x)^3(5y)^0
(6x)^3(5y)^0
Change
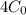 into the format of the Combination Formula
into the format of the Combination Formula
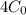 = 4!/ 4! - (4! - 0!)
= 4!/ 4! - (4! - 0!)
Now plug this back into our equation
- = (4!/(4! - 4!)) (6x)^3(5y)^0
- = (4!/0) (6x)^3
- undefined
There is no term containing x^3 based on the fact that
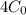 is undefined.
is undefined.
I hope that you can figure out Combinations. I remember learning about them, but it is a very conceptual concept. Once you do figure out how they work though, they become very easy to use. Good luck on your math.